按赞
反对
7
收藏
分享
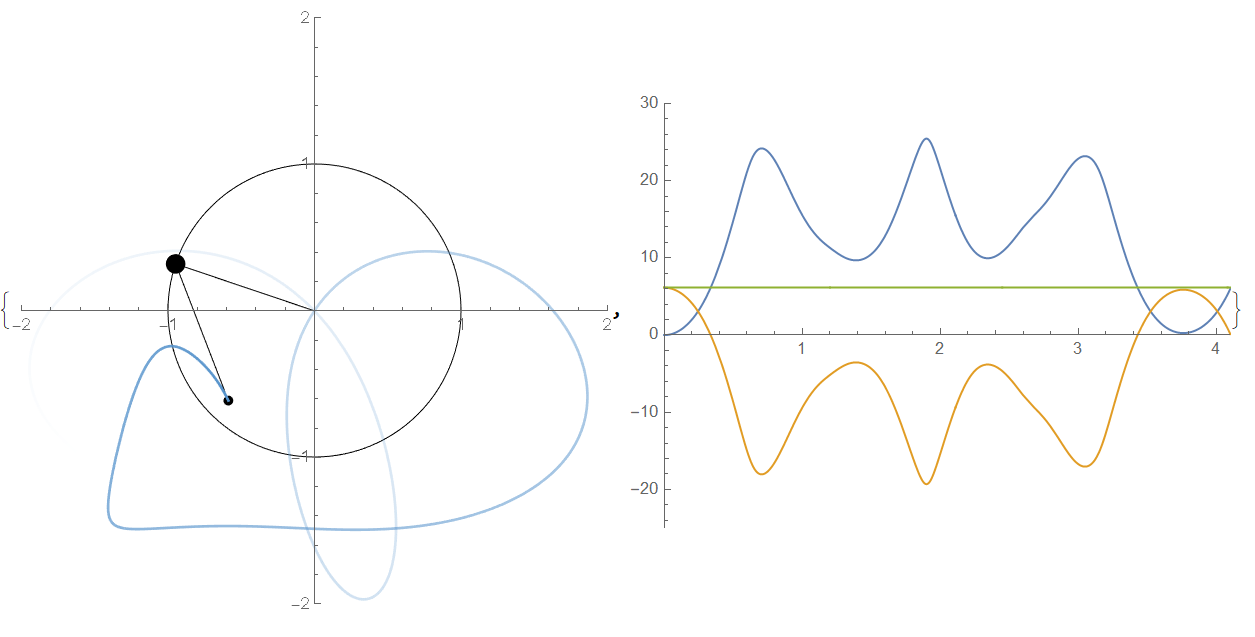
Wolfram Mathematica 混沌摆模拟以及可视化
 Clear["Global`*"];
(*定义参数*)
{g, l1, l2, m1, m2, tt} = {9.8, 1, 1, 1, 3, 100};
(*定义拉格朗日方程*)
L = (m1 + m2)/2 l1^2 (a'[t])^2 + m2/2 l2^2 (b'[t])^2 +
m2*l1*l2*a'[t]*b'[t]*Cos[a[t] - b[t]] + (m1 + m2)*g*l1*Cos[a[t]] +
m2*g*l2*Cos[b[t]];
(*定义微分方程以及合适的边界条件*)
funcs = {D[L, a[t]] == D[D[L, a'[t]], t],
D[L, b[t]] == D[D[L, b'[t]], t], a[0] == 3 Pi/4, b[0] == Pi/6,
a'[0] == 0, b'[0] == 0};
(*微分方程的100精度数字解*)
sov = NDSolve[funcs, {a, b}, {t, 0, tt}, PrecisionGoal -> 100][[1]];
(*随时间变化的角度*)
a = a /. sov;
b = b /. sov;
(*整个系统的动量,机械能*)
T[t_] := (m1 + m2)/2 l1^2 ((D[a[x], x]) /. x -> t)^2 +
m2/2 l2^2 ((D[b[x], x]) /. x -> t)^2 +
m2*l1*l2*((D[a[x], x]) /. x -> t)*((D[b[x], x]) /. x -> t)*
Cos[a[t] - b[t]];
V[t_] := -(m1 + m2)*g*l1*Cos[a[t]] - m2*g*l2*Cos[b[t]];
Energy[t_] := T[t] + V[t];
(*m1和m2的坐标*)
p1[t_] := {l1*Sin[a[t]], -l1*Cos[a[t]]};
p2[t_] := {l1*Sin[a[t]] + l2*Sin[b[t]], -l1*Cos[a[t]] - l2*Cos[b[t]]};
(*可视化模块*)
result = Animate[{Show[
Graphics[Circle[{0, 0}, 1], PlotRange -> {{-2, 2}, {-2, 2}},
AxesOrigin -> {0, 0}, Axes -> True, Frame -> False,
ImageSize -> Medium],
Graphics[{Line[{{0, 0}, p1[u], p2[u]}], Disk[p1[u], m1/15],
Disk[p2[u], m2/15]}],
If[u < 3,
ParametricPlot[p2[t], {t, 0, u},
ColorFunction ->
Function[{x, y, u}, f = Hue[0.58, 0.58, 0.8, u]]],
ParametricPlot[p2[t], {t, u - 3, u},
ColorFunction ->
Function[{x, y, u}, f = Hue[0.58, 0.58, 0.8, u]]]]],
ParametricPlot[{{t, T[t]}, {t, V[t]}, {t, Energy[t]}}, {t, 0, u},
ImageSize -> Medium, AspectRatio -> 0.75,
PlotRange -> {{0, u}, {-25, 30}}]}, {u, 0.01, tt, 0.01},
AnimationDirection -> Forward, RefreshRate -> 180,
DefaultDuration -> tt]
Clear["Global`*"];
(*定义参数*)
{g, l1, l2, m1, m2, tt} = {9.8, 1, 1, 1, 3, 100};
(*定义拉格朗日方程*)
L = (m1 + m2)/2 l1^2 (a'[t])^2 + m2/2 l2^2 (b'[t])^2 +
m2*l1*l2*a'[t]*b'[t]*Cos[a[t] - b[t]] + (m1 + m2)*g*l1*Cos[a[t]] +
m2*g*l2*Cos[b[t]];
(*定义微分方程以及合适的边界条件*)
funcs = {D[L, a[t]] == D[D[L, a'[t]], t],
D[L, b[t]] == D[D[L, b'[t]], t], a[0] == 3 Pi/4, b[0] == Pi/6,
a'[0] == 0, b'[0] == 0};
(*微分方程的100精度数字解*)
sov = NDSolve[funcs, {a, b}, {t, 0, tt}, PrecisionGoal -> 100][[1]];
(*随时间变化的角度*)
a = a /. sov;
b = b /. sov;
(*整个系统的动量,机械能*)
T[t_] := (m1 + m2)/2 l1^2 ((D[a[x], x]) /. x -> t)^2 +
m2/2 l2^2 ((D[b[x], x]) /. x -> t)^2 +
m2*l1*l2*((D[a[x], x]) /. x -> t)*((D[b[x], x]) /. x -> t)*
Cos[a[t] - b[t]];
V[t_] := -(m1 + m2)*g*l1*Cos[a[t]] - m2*g*l2*Cos[b[t]];
Energy[t_] := T[t] + V[t];
(*m1和m2的坐标*)
p1[t_] := {l1*Sin[a[t]], -l1*Cos[a[t]]};
p2[t_] := {l1*Sin[a[t]] + l2*Sin[b[t]], -l1*Cos[a[t]] - l2*Cos[b[t]]};
(*可视化模块*)
result = Animate[{Show[
Graphics[Circle[{0, 0}, 1], PlotRange -> {{-2, 2}, {-2, 2}},
AxesOrigin -> {0, 0}, Axes -> True, Frame -> False,
ImageSize -> Medium],
Graphics[{Line[{{0, 0}, p1[u], p2[u]}], Disk[p1[u], m1/15],
Disk[p2[u], m2/15]}],
If[u < 3,
ParametricPlot[p2[t], {t, 0, u},
ColorFunction ->
Function[{x, y, u}, f = Hue[0.58, 0.58, 0.8, u]]],
ParametricPlot[p2[t], {t, u - 3, u},
ColorFunction ->
Function[{x, y, u}, f = Hue[0.58, 0.58, 0.8, u]]]]],
ParametricPlot[{{t, T[t]}, {t, V[t]}, {t, Energy[t]}}, {t, 0, u},
ImageSize -> Medium, AspectRatio -> 0.75,
PlotRange -> {{0, u}, {-25, 30}}]}, {u, 0.01, tt, 0.01},
AnimationDirection -> Forward, RefreshRate -> 180,
DefaultDuration -> tt]声明本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得UP主同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理: DMCA投诉/Report













这个咔友似乎很害羞(bushi
这个人确实想隐藏自己(大概
这个咔友似乎很害羞(bushi
Howdy!
*”]; 里为什么用中文引号?</li><li>NDSolve::ndnum: 在 t == 0.处碰到一个导数的非数值量.在Wolfram Mathematica 12.3.1 for Mac OS X ARM (64-bit) (July 24, 2021)
求包养